The SuperWheel: the next magical energy harvester?
In the history of science, there have been many claims for seemingly impossible technological achievements. The Perpetuum Mobile (everlasting motion) machine is like the Philosophers’ Stone that turns lead into gold: many have searched for it, but science says there is no needle in the haystack. Nevertheless, some seemingly impossible inventions have been realised; airplanes are heavier than air, yet they can fly. Heat pumps can work at an efficiency of well above 100% [1](see Reden Makes Sense).
If an invention seems impossible, a working prototype can show that our intuition is misleading. If it works after all, there is a challenge for science. A bumble bee can fly, so if aerodynamics and biology indicate that it can’t, aerodynamics and biology should do their homework.
The SuperWheel is a mechanical device which promises to reduce the effort needed to propel a bicycle.

It works in a way which is described somewhat vaguely on the website. A European patent was granted (EP3700807), to which I refer readers who’d like to try making sense of the mechanics. Reden Makes Sense tries to show that numbers are essential in any innovation. Let’s look at the physics of a bicycle moving over a road with bumps, and see if a SuperWheel could work at all. Which energy is available for the SuperWheel to help the cyclist move forward?
Bumps and energy
It is easier to cycle on a smooth tarmac road than on a very bumpy road. What is the underlying physical cause? For simplicity, we assume the bicycle to be elastic and the rider to be a passive mass. This leads to a simple mass-spring system.
What happens if this simple system is moving along a smooth road when it encounters a simplified bump?
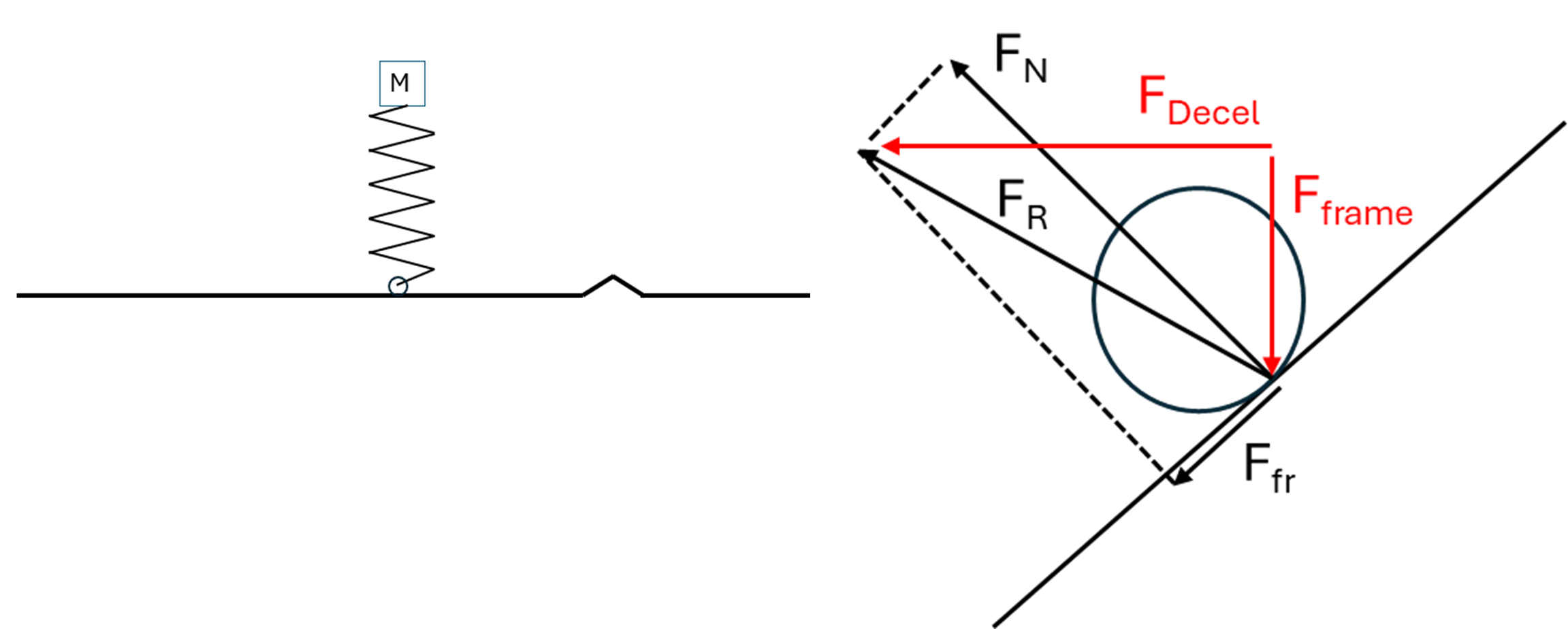
When the wheel moves uphill, there is a force component (Fdecel) which slows down the bicycle. At the same time, the wheel moves up and compresses the spring (the mass takes time to start moving). In energy terms, kinetic energy from the forward motion is converted to elastic energy. Once the mass starts moving, the system will oscillate, with constant exchange between kinetic energy, elastic energy and potential energy (because of gravity). But what happens on the downward slope? And how much energy is involved? On the downward slope, there is an accelerating force, so the forward speed increases. If the bump is exactly right for the system, no oscillation is caused, and the forward speed is restored, but in general, forward velocity is lost and vertical oscillation is what comes in its place.
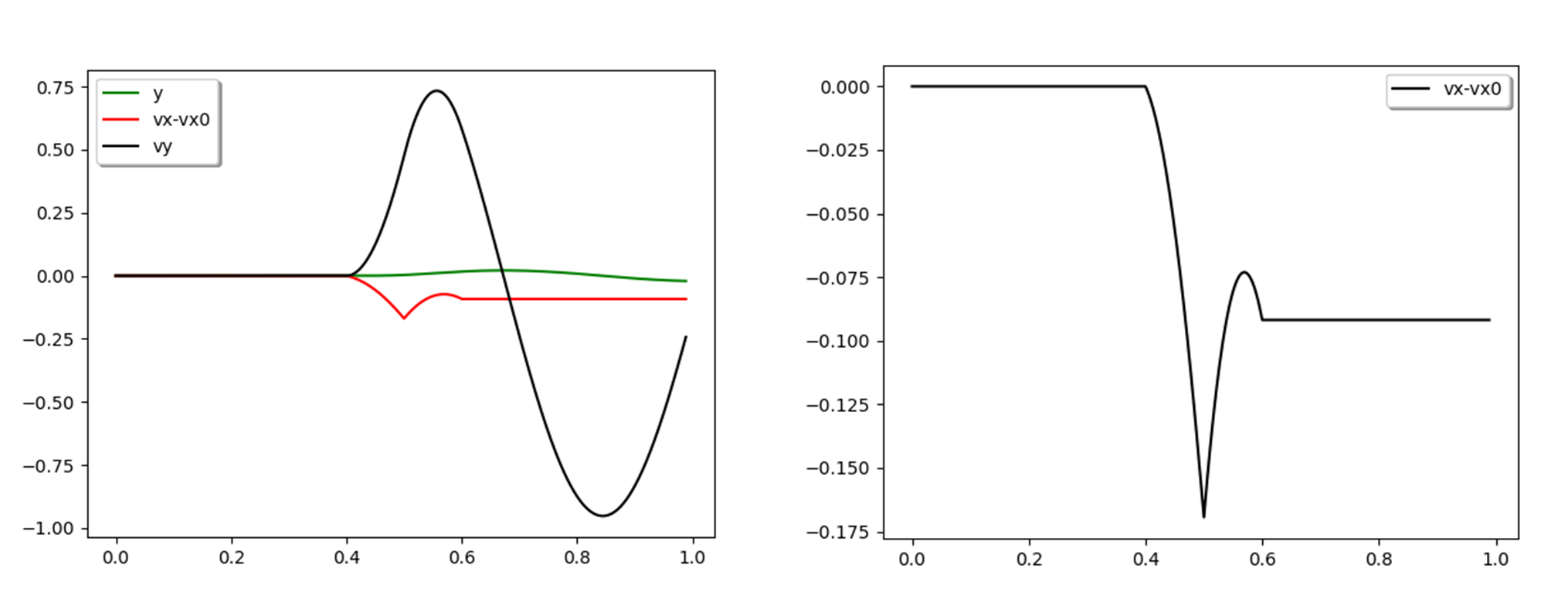
Right: The slight decrease in speed after this single bump
If the bump is exactly the right size for the system, then the mass will move up, then down again after passing the bump,and the deceleration on the way up will be the same as the acceleration after the bump. The mass will continue to move in a straight line, without oscillation. In the general case, however, the speed of the mass (in the horizontal direction) will be reduced, and the mass will oscillate. A part of the kinetic energy of the forward motion is now present in the form of vertical oscillation. In practice, the vertical oscillation is reduced (by the tyres and, in cars, by the shock absorbers) by converting kinetic energy into heat. If the SuperWheel can prevent this, then it could lead to a higher efficiency.
Time for some numbers
First, we’d like to know how much energy is involved. For the order of magnitude, a simple case is good enough. For bumps of 25 mm high, 0.5 m apart, with a slope of 45 degrees, and a bicycle speed of 5m/s, a mass (with rider) of 100 kg, and an initial ‘compression’ of 10 mm:
The bicycle encounters 10 bumps per second.The total lift (and total drop) is 0.25 m per second. The vertical force on the upward slope is of order 1000 N (the force on the down slope is a little less),and the horizontal force must be the same as the vertical force, due to the 45-degreeslope.
The power delivered vertically is roughly 1000N*0.25 m/s or 250 W. This is not a negligible number for a bicycle (an e-bike motor often has this power). However, if we stick to the same simplification,the power on the down slope is exactly the same, but with the opposite sign. We must make it a bit more complex. A simulation for a single bump, in which the equations of motion for the mass are solved, gives the result shown in the graphs. The horizontal velocity is reduced by 0.09 m/s (0.3 km/h) by a single bump. If 10 bumps are encountered per second, this would slow the bicycle down by 3 km/h per second, unless more effort is put in: (10*0.09 m/s)/s * 100 kg = 90W)
(How) does the SuperWheel work?
The explanation on the website of SuperWheel is not convincing. The claimed weight-to-energy-conversion is highly dubious, if only because weight is measured in Newtons (N) and energy in Joules(J = N*m). If the weight is allowed to act over a distance, then it performs energy. The SuperWheel, however, allows the bicycle to drop a little when the rider mounts (perhaps 25 mm, which corresponds to something in the order of1000 N * 0.025 m = 2.5 J), but after that, the height is constant, so no energy is derived from the weight. If anything, the mechanism leads extra friction. The mechanism does not have any elements which take advantage of the dynamic effect described above.
The SuperWheel website contains a video which aims to demonstrate the SuperWheel effect. The bicycle is repeatedly pushed down, and then lifted. There is an extremely slow rotation of the wheel afterwards. The rotation is so slow that it may be caused by a slight forward motion of the frame while lifting. In any case, it would have cost much less effort to spin the wheel directly than to push down on the frame repeatedly,with considerable force.
What about the cycling tests?
On the French Superwheel site, there is a report of actual cycling tests. These appear to show that less energy is required from the user when he uses a SuperWheel. There are several strange points about these tests. First, the tyre pressure is 6.5 bar for the SuperWheel, and 4 bar for the normal wheel. The reason given is that SuperWheel works best with a high pressure. However, the normal wheel would also profit from the higher pressure. In this study, the rolling resistance of their bicycletyre would increase by 26% if the pressure is reduced from 6.5 to 4 bar. It would be interesting, therefore, to see the results in tests with equal tyre pressures. The test claims a lower positive effect for the SuperWheel at lower speeds, and this would be expected as rolling resistance plays a larger part at lower speeds; at high speeds, aerodynamic drag dominates.
Secondly, the energy is measured using a power meter in the crank. This measures the energy provided by the cyclist through the pedals. It is possible that the SuperWheel mechanism, somehow,converts the up and down movement of the rider to forward motion, thus bypassing the power meter. If that is the case, the rider still provides the same energy, but only a part of it is recorded by the power meter.
The cycling tests do not give useful results, but they do convey the enthusiasm of the tester. Is it really merely the higher tyre pressure?
Conclusion
Bumpy roads slow down cyclists because the energy spent to ‘climb’ the bumps is not recovered, but converted to heat. A mechanism that prevents this would help. The numbers from a simple model show it could be an interesting amount of energy for a cyclist. The SuperWheel mechanism is neither aimed at nor equipped to use this energy. Without a better explanation or better tests, its effectiveness cannot be accepted.
The good news is that, for now, a bicycle ride will continue to be a good physical exercise for your health. However, as in many ‘crazy’ inventions from the past, the SuperWheel points to a physical opportunity, and may inspire someone to invent a ‘hyper’-wheel that actually works. We recommend this someone to start from the physics, and look at the numbers.
[1]: The definition of efficiency matters; a heat pump with a COP of 4 can pump 4 times more energy into a building than it draws from the electricity grid. The exergetic efficiency of a heat pump is much less than 100 %. The heat pump uses energy from the environment that is free. It uses one unit of energy to upgrade three units of energy from ambient temperature to a useful temperature.



